Bài toán của học sinh tiểu học hay THCS gì đó

quangduong · August 29, 2017, 6:32pm

Hôm nay trên fb, trong một group về toán, mình thấy có một bài toán cho học sinh tiểu học như thế này:
(mình gõ cả đề và up cả ảnh)
Cho 9 chữ số từ 1 đến 9, đặt 9 chữ số này vào 9 ô trống sao cho:
a/(bc) + d/(ef) + g/(hi) = 1
trong đó a,b,c,d,e,f,g,h,i là các ô để đặt 9 chữ số đó.
Lưu ý bc là số có hàng chục là b và hàng đơn vị là c, không phải tích hai số b và c.

Đây là một bài toán mà bất cứ ai đã học lập trình đều nhận thấy là phải dùng máy tính mới làm được, chứ suy luận toán học thì ra kiểu gì và bao giờ mới ra

. Đề thi học sinh giỏi mất chất quá, chắc là để tìm máy tính chứ không phải tìm nhân tài

Đáp án của bài toán là 5,3,4,7,6,8,9,1,2.
Thấy bài toán này mình cũng đã thử 9 vòng lặp lồng nhau. Nhưng không được như mong đợi.
Nếu sử dụng một ngôn ngữ lập trình thì nên làm thế nào mới được và làm sao thì nhanh nhất đây?
Hóng mọi người vào thảo luận…

noname00 · August 29, 2017, 6:58pm

Giá trị của 9 ô đó là hoán vị của {1, 2, 3,… , 9}. Ta sinh ra 9! dãy hoán vị (1 số NNLT có hàm sẵn, còn 1 số khác phải viết tay) với

a[] = permutation(1, 2,..., 9)
            a[0]               a[3]               a[6]
res = ---------------- + ---------------- + ----------------
      a[1] * 10 + a[2]   a[4] * 10 + a[5]   a[7] * 10 + a[8]

vtrnnhlinh · August 30, 2017, 6:46am

hồi tiểu học em đi thi hsg toán cũng gặp bài tương tự như thế này, thế là để bài đó làm cuối, thử tới thử lui ra kết quả chớ éo biết cách làm, ghi đáp án chí ít cũng được 0.5đ

drgnz · August 30, 2017, 8:11am

Nhìn KQ nên đoán bừa chiến thuật ntn :))

Tìm số lớn nhất có thể tạo ra từ 9 số trên
Ta biến tử càng lớn, mẫu càng nhỏ số càng lớn
~> 9/12 = 0.75
-> ta cần tìm tổng 2 số còn lại sao cho = 0.25

0.25 có thể = 0.1 + 0.15
0.2 + 0.05
= 0.125 + 0.125
v.v

Vì sao chọn chọn số lớn nhất, vì để phần còn tìm nhỏ lại, từ đó dễ tìm hơn. Như trên 0.25 sẽ dễ phân tích hơn phần nào so với 0.75 (vì sẽ có nhiều khả năng 2 số tổng ra 0.75 ở dạng “đẹp” hơn)

Vd trường hợp 0.1 + 0.15
Tìm 0.1

Ta biết a/b ~ 1 khi a > b, và a -> b
a/b ~ 1
-> (a / b) / 10 ~ 0.1
-> a / 10*b ~ 0.1
Vậy tìm bừa a, b sao cho a > b và gần b nhất
ta có
(8, 7); (7, 6) …
Thử 8/76, 8/75, …

còn lại 345 phải gom sao cho ra 0.15 (vd chọn 8/76)
-> c/d*10 ~ 0.15 thì c > d. Mà do 0.15 nên có thể sao cho c và d hơi gần nhau chứ ko cần quá gần =))
-> (4, 3); (5, 4); (5, 3)
Thử (4, 3) -> 4/35
4/35 + 8/76 = (tất nhiên ko phải 0.25 ròi :)) )

Thử dần thì sẽ ra được kq trên \ :v /

noname00 · November 18, 2019, 4:14am

Mình có thử làm theo cách toán học 1 chút, tuy nhiên vẫn bị mắc. Chắc vẫn phải mò đáp số như @drgnz.

Đưa phép tính của đề bài thành

a / b + c / d + e / f = 1
(0 < a, c, e < 10 < b, d, f < 100
(10 <= b, d, f, nhưng vì không được có chữ số 0 nên 10 < b, d, f)

Giả sử b <= d <= f
-> $1=\frac{a}{b}+\frac{c}{d}+\frac{e}{f}<\frac{10}{b}+\frac{10}{d}+\frac{10}{f}<=\frac{10}{b}\cdot 3=\frac{30}{b}$

-> b < 30

Bên cạnh đó
$1=\frac{a}{b}+\frac{c}{d}+\frac{e}{f}<=\frac{a}{b}+\frac{c}{b}+\frac{e}{b}<=\frac{a+c+e}{b}$

-> b <= a + c + e

Mà a, c, e phân biệt và đều < 10 nên

max{a + c + e} = 9 + 8 + 7 = 24
-> b <= a + c + e <= 24

Vì b > 10, b có 2 chữ số phân biệt nên 12 <= b <= 24.

TH1. `12 <= b < 20`, mà `9 >= a > 1` (b đã có chữ số 1, nên a không thể bằng 1)

-> d không thể dùng chữ số 1 làm chữ số hàng chục, mà d >= b -> d > 20 (d != 20 vì không có chữ số 0)
Thêm nữa, d != 21 (b có chữ số 1), d != 22 (không có 2 chữ số giống nhau) -> d >= 23.
Ta cũng chứng minh được f >= 32.

Nếu b = 12 thì d > 30 -> f > 40.

-> $\frac{9}{12}>=\frac{a}{b}>=\frac{2}{19}$ -> $\frac{1}{4}<=\frac{c}{d}+\frac{e}{f}<=\frac{17}{19}$

-> $\frac{1}{4}<=\frac{c}{d}+\frac{e}{f}<=\frac{c+e}{d} \rightarrow d<=4(c+e)<=4(9+8)=68$

$\frac{17}{19}>=\frac{c}{d}+\frac{e}{f}>=\frac{c+e}{f} \rightarrow 17f>=19(c+e)$

$\frac{1}{4}<=\frac{c}{d}+\frac{e}{f}<\frac{10}{d}+\frac{10}{f} \rightarrow \frac{1}{d}+\frac{1}{f}>\frac{1}{40}$

Đến đây có thể mò nghiệm

TH2. `20 < b <= 24` (không có chữ số 0 -> `b != 20`)

-> $\frac{a}{b}<\frac{10}{20}=\frac{1}{2}$

-> $\frac{1}{2}<\frac{c}{d}+\frac{e}{f}<=\frac{c+e}{d} \rightarrow d<2(c+e)<=2(9+8)=34$

b <= d < 34, mà d không thể có chữ số 2 ở hàng chục (do b đã có chữ số 2) -> 30 < d < 34, d != 32, d != 33 -> d = 31
-> b != 23 do d đã có chữ số 3 ở hàng chục, b != 22
-> (b, d) = (24, 31)

Ta có thể chứng minh được f > 50.

Tương tự TH trên, suy ra được $\frac{1}{20}<\frac{1}{d}+\frac{1}{f}$

$d=31\rightarrow \frac{1}{f}>\frac{1}{20}-\frac{1}{d}=\frac{1}{20}-\frac{1}{31}=\frac{11}{620} \rightarrow f<\frac{620}{11}\rightarrow 50<f<=56$

Mà f != 51, 52, 53, 54, 55 -> f = 56.

-> a, c, e thuộc {7, 8, 9}
-> Mò nốt. Mà trường hợp này cũng vô nghiệm.

p/s: Anh @ltd ơi cho viết latex trên DNH đi anh

quangduong · August 30, 2017, 10:31am

Mình không rành về thuật toán. Qua việc sinh hoán vị mà HK boy đề cập thì mình mới biết.
Mình nhận định là với kiến thức toán tiểu học thì không ai làm được bài này, trừ khi có đủ thời gian để … thử.
Thấy mọi người thảo luận nên mình cũng góp ý tưởng - cụ thể là làm giảm thiểu tối đa số trường hợp cần xét. Nhưng mà suy luận rất phức tạp!

Đầu tiên, mình phát biểu bài toán theo kiểu khác:
Tìm các số tự nhiên a,b,c,x,y,z sao cho a,b,c có 1 chữ số; x,y,z, có 2 chữ số, 9 chữ số của a,b,c,x,y,z có đủ các chữ số từ 1 đến 9 và thỏa mãn hệ thức:
$\frac{a}{x}+\frac{b}{y}+\frac{c}{z} = 1$
Biến đổi tương đương, phương trình trở thành:
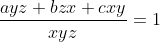
$\frac{ayz+bzx+cxy}{xyz}=1$
x,y,z là các số không vượt quá 98 nên ước nguyên tố của x,y,z chỉ có thể nhận các giá trị là: {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97}
Đầu tiên, loại bớt những ước nguyên tố có hai chữ số:
ayz+bzx+cxy = xyz nên ayz+bzx+cxy chia hết cho x, tức là ayz chia hết cho x. Mà x có 2 chữ số, mà a có 1 chữ số nên nếu như x có ước nguyên tố có 2 chữ số thì chịu, bù vào đó yz sẽ chia hết cho ước nguyên tố q đó. yz chia hết cho số nguyên tố q thì y chia hết cho q hoặc là z chia hết cho q.
+) q=11 thì ta loại luôn vì bội của nó có hai chữ số giống nhau
+) q=37 thì x = 37 hoặc 74, y hoặc z cũng chỉ nhận 37 hoặc 74, trùng số 7, loại
+) q=47 thì x = 47 hoặc 94, y hoặc z cũng chỉ nhận 47 hoặc 94, trùng số 4 nên loại.
+) q>47 thì loại ngay vì bội hoặc là q hoặc 2q mà 2q thì đã có 3 chữ số mất rồi.
Như vậy các số x,y,z chỉ có thể có các ước nguyên tố là 2,3,5,7,13,17,19,23,29,31,41,43 và chỉ cần 1 số có ước nguyên tố là p thì 1 trong 2 số còn lại cũng phải chia hết cho p.
Một số khi phân tích nguyên tố thì thường sẽ có nhiều hơn 1 ước nguyên tố. Do vậy hãy xem các cặp nguyên tố nào không thể kết hợp được. Thật may mắn, nếu như trong các ước nguyên tố của x,y,z mà có hai ước nguyên tố có 2 chữ số thì phải có 1 số trong x,y,z chia hết cho cả hai ước nguyên tố đó. Mà tích hai ước nguyên tố có 2 chữ số thì lúc nào cũng quá 100 rồi. Vậy x,y,z nhiều nhất chỉ có 1 ước nguyên tố có 2 chữ số thôi.
Đến đây thì ta đã biết chỉ có thể kết hợp các ước nguyên tố 1 chữ số cùng với đúng 1 ước nguyên tố 2 chữ số để làm điều này. Giờ thì số trường hợp cần phải xét cũng đã được giảm đi đáng kể rồi

Bài toán của học sinh tiểu học hay THCS gì đó

TH1. 12 <= b < 20, mà 9 >= a > 1 (b đã có chữ số 1, nên a không thể bằng 1)

TH2. 20 < b <= 24 (không có chữ số 0 -> b != 20)

TH1. `12 <= b < 20`, mà `9 >= a > 1` (b đã có chữ số 1, nên a không thể bằng 1)

TH2. `20 < b <= 24` (không có chữ số 0 -> `b != 20`)