Hỏi ý tưởng bài toán đếm số cách chọn vật cho vào túi

[haitu]

Naruto có N cái túi, túi thứ i có Ai đồng tiền. Mỗi lần đi làm nhiệm vụ, Naruto sẽ chọn ra một số túi để mang theo nếu thỏa mãn điều kiện sau:

Mọi người cho mình hỏi ý tưởng của bài này với ạ

[rogp10]

Chỉ cần hai biến đại diện cho số dư 0 và số dư 1, rồi duyệt mảng.

[haitu]

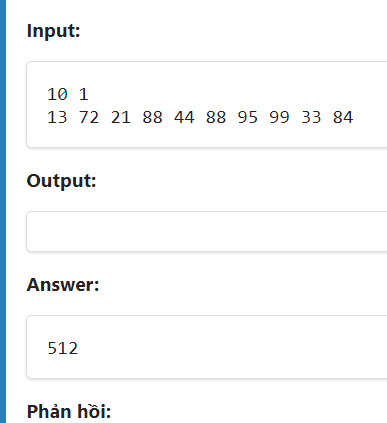
bạn nói rõ hơn chút được không ạ?
ý tưởng của m là tính tổng của 2,3,4 đến n phần tử trong mảng nhưng làm thế phải tạo n vòng lặp for.
nên m nghĩ cách này không đúng.

[kisuluoibieng (Tên Gì Cũng Được)]

Nhận xét,
Khi lấy thêm một túi có số đồng tiền là chẵn, thì sẽ không anh hưởng đến kết quả %2, nên chỉ cần xét cách chọn số lượng túi chứa số đồng tiền là lẻ (sau đây gọi là túi chẵn túi lẻ cho gọn)

Gọi số lượng túi chẵn là C, số lượng túi lẻ là L
Ta luôn có công thức chọn số lượng túi như sau

x túi chẵn + y túi lẻ

x: vì số lượng túi chẵn không ảnh hưởng đến kết quả, nên có thể chọn từ 0 đến C
y: có dạng 2k (P = 0) hoặc 2k+1 (P = 1), và tất nhiên là chọn cũng không quá L

vì cách chọn túi chẵn và cách chọn túi lẻ là độc lập với nhau, nên kết quả sẽ là
[số cách chọn túi chẵn] x [số cách chọn túi lẻ]

Số cách chọn túi chẵn thì có thể chọn 0 1 2 … C túi, như vậy kết quả sẽ là 2^C (tổng tổ hợp 0 đến chập C của C)
Số cách chọn túi lẻ thì sẽ là tổng các tổ hợp chập lẻ hoặc tổ hợp chập chẵn của L

ở đây chưa rõ là không chọn túi nào thì có tính là 1 cách chọn hay không nên tùy yêu cầu mà có thể khác chút (chắc là trừ đi 1 với P chẵn)

[tntxtnt]

tổng các tổ hợp chập lẻ / tổng tổ hợp chập chẵn của L là 2^{y-1} nha

chứng minh: ta có

\begin{aligned} (1 - 1)^n &= (1 + (-1))^n \\ 0 &= {n \choose 0}1^{n}(-1)^{0} + {n \choose 1}1^{n-1}(-1)^{1} + {n \choose 2}1^{n-2}(-1)^{2} + ... + {n \choose k}1^{n-k}(-1)^{k} + ... + {n \choose n}1^{0}(-1)^{n} \\ 0 &= {n \choose 0} - {n \choose 1} + {n \choose 2} - ... + (-1)^k{n \choose k} + ... + (-1)^n{n \choose n} \\ {n \choose 1} + {n \choose 3} + {n \choose 5} + ... &= {n \choose 0} + {n \choose 2} + {n \choose 4} + ... \end{aligned}

hay tổng các tổ hợp chập lẻ = tổng tổ hợp chập chẵn, mà tổng các tổ hợp là 2^n rồi vậy tổng các tổ hợp chập lẻ = tổng tổ hợp chập chẵn = 2^{n-1}

trường hợp n = 0 thì ta có (1 - 1)^0 = 0^0 có lẽ kết quả khác 0 nên công thức này ko đúng nha

vậy bài này đếm nếu có tập lẻ thì đáp án là 2^{N-1} bất chấp P là bao nhiêu, còn nếu ko có tập lẻ thì đáp án là 0 nếu P = 1, 2^N nếu P = 0

đây cũng có lẽ là 1 cách chứng minh 0^0 = 1

ơ bấm máy tính 0^0 nó ra error

[kisuluoibieng (Tên Gì Cũng Được)]

Vậy chốt lại đáp án là
2^(C + L - 1)
với C là số lượng túi chẵn và L là số lượng túi lẻ rồi (có thể khác tí tùy theo điều kiện có được không chọn túi nào hay không mà thôi)

[rogp10]

Tổ hợp mà, 0⁰ là 1 thôi.