Đếm số phép toán sắp xếp

Nobita004 · May 15, 2019, 11:17am

Cho em hỏi thuật toán bài dưới được không ạ! Em cảm ơn!

Bài Toán:
Với một chồng sách hiện tại ta phải sắp xếp sao cho chiều rộng của chồng sách giảm dần từ dưới lên trên, chỉ có một thao tác chuyển sách duy nhất là ta sẽ đi từ trên xuống dưới nếu thấy một quyển sách nào có chiều rộng nhỏ hơn quyển sách ngay bên trên nó thì ta sẽ nhấc quyển sách đó lên và đặt lên trên đầu chồng sách, cứ làm như vậy đến khi nào không còn quyển sách nào lỗi nữa thì thôi. Vậy đấy, quả thực công việc không hề đơn giản chút nào cả, chính vì thế nên chủ hiệu sách trả rất nhiều tiền cho ai làm công việc đó. Anh M chấp nhận làm công việc đó để có thể kiếm được nhiều tiền, và tất nhiên nhiều tiền thì sẽ có khả năng tán được em Hot Girl đó. Anh M muốn biết trước với chồng sách sắp phải sắp xếp anh M phải thực hiện bao nhiêu lần chuyển sách để được chồng sách đúng như yêu cầu, đương nhiên với khả năng lập trình của mình anh M đã quyết định lập trình giải quyết bài toán đó, nhưng khi bắt đầu vào lập trình anh M mới phát hiện ra đây quả thật cũng là một bài toán không hề đơn giản, hèn nào chủ hiệu sách lại chả nhiều tiên cho công việc này như vậy.

Yêu cầu: Cho n là số lượng sách của chồng sách và dãy n phần tử là chiều rộng của chồng sách tính từ trên xuống dưới. Hãy giúp anh M tính toán số lượng lần cần chuyển sách.

Dữ liệu : Vào từ file văn bản SORT.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương duy nhất n (1 ≤ n ≤ 105)

• Dòng thứ hai chứa n số nguyên dương a i là chiều rộng của các cuốn sách ( a i ≤ 109 )

Kết quả : Ghi ra file văn bản SORT.OUT một số duy nhất là kết quả tìm được, lấy số dư cho 109+7.

SORT.INP	SORT.OUT
5 1 1 2 4 3	6

Nobita004 · May 14, 2019, 10:13am

Độ phức tạp ở đây là O(n log n) . Còn sharker sort là O(n^2) liệu có chạy được không anh?

hungaya · May 14, 2019, 1:37pm

Phải sắp xếp như thế này không? Mình không hiểu đề lắm.

int naive_sort(int* arr, int len) {
    int count = 0;
    int i = 0, end = len-1;
    
    while (i < end) {
        while (i < end && arr[i] <= arr[i+1]) {
           i++;
        }
        
        if (i < end) {
            int temp = arr[i+1];
            for (int j = i+1; j > 0; j--) {
                arr[j] = arr[j-1];
            }
            arr[0] = temp;
            
            i = 0;
            count++;
        }
    }
    
    return count;
}

Link: https://ideone.com/eY9P4a

Nobita004 · May 14, 2019, 3:17pm

Kiểu giống như thế này đó anh! Nhưng độ phức tạp của bài toán là O(n log n) nên có lẽ code này không full được ạ!

hungaya · May 14, 2019, 4:00pm

Không thấy mình ghi là naive_sort() á.
Mình viết sort này chỉ để kiểm tra cái sort khác xịn hơn thôi.

rogp10 · May 14, 2019, 5:35pm

5 1 1 2 4 3

2 1 1 5 * * (3 lần)
1 1 2 * * * (2 lần)
4 1 1 2 5 * (1 lần)
2 1 1 4 * * (2 lần)
1 1 2 4 * * (2 lần)
…
sao ra 6 được nhỉ.

Nobita004 · May 15, 2019, 10:44am

Anh ơi, 5 đây là n (tức số chồng sách) chứ không phải là bề rộng của 1 quyển sách!

hungaya · May 19, 2019, 11:58am

Xong, kiểm tra thử đúng không.
Chủ yếu tốn thời gian implement AVL Tree :v

Trong cả đống code chỉ có đoạn này quan trọng nhất.
Thao tác với tree luôn là O(logn), cộng thêm cái vòng for ở ngoài nữa là O(n). Tổng cộng O(n.logn).

for (int i = last_index+1; i < arr.size(); i++) {
    if (arr[i].first < tree.max()) {
        count += arr[i].second;
        count += tree.count(arr[i].first);
        tree.insert(arr[i].first, arr[i].second);
    }
}

Full code thì xem thêm link

hungaya · May 19, 2019, 11:58am

Phần giải thích code, tại nó dài quá, nên viết nháp rồi sửa đi sửa lại. Cuối cùng đăng trễ. :v

Đổi cái mảng số nguyên thành mảng các pair. Giá trị thứ nhất là số nguyên key, giá trị thứ 2 là số lần lặp key trong mảng ban đầu. Ví dụ:

1 1 1 4 4 2 3 3 3 3
(1,3) (4,2) (2,1) (3,4)

2 2 2 2 2
(2,5)

4 3 5 1
(4,1) (3,1) (5,1) (1,1)

Thay vì sort mảng số nguyên, thì sort mảng các pair rồi chuyển sang lại mảng số nguyên.

(1,3) (2,1) (3,4) (4,2)
1 1 1 2 3 3 3 3 4 4

(2,5)
2 2 2 2 2

(1,1) (3,1) (4,1) (5,1)
1 3 4 5

Xét một mảng các pair có dạng: (b, l) (a₁, l₁) (a₂, l₂) … (a_n, l_n), trong đó:

a₁ < a₂ < … < a_n < b,
a_i, b, n là số nguyên dương.

Sau khi sort dãy trên, có được mảng: (a₁, l₁) (a₂, l₂) … (a_n, l_n) (b, l).
Gọi tổng số lần chuyển a_i lên đầu mảng trong khi sort là T(n).

Trường hợp n = 1: (b, l) (a₁, l₁)

(a₁, 1) (b, l) (a₁, l₁ - 1), vì b > a₁, có 1 bước
(a₁, 2) (b, l) (a₁, l₁ - 2), có 1 bước
…
(a₁, l₁ - 1) (b, l) (a₁, 1), có 1 bước
(a₁, l₁) (b, l), có 1 bước

Tổng cộng T(1) = l₁

Trường hợp n = 2: (b, l) (a₁, l₁) (a₂, l₂)

(a₁, l₁) (b, l) (a₂, l₂), vì b > a₁, có l₁ bước

(a₂, 1) (a₁, l₁) (b, l) (a₂, l₂ - 1), vì b > a₂, có 1 bước
(a₁, l₁) (a₂, 1) (b, l) (a₂, l₂ - 1), vì a₂ > a₁, có l₁ bước
(a₂, 1) (a₁, l₁) (a₂, 1) (b, l) (a₂, l₂ - 2), vì b > a₂, có 1 bước
(a₁, l₁) (a₂, 2) (b, l) (a₂, l₂ - 2), vì a₂ > a₁, có l₁ bước
…
(a₂, 1) (a₁, l₁) (a₂, l₂ - 1) (b l), có 1 bước
(a₁, l₁) (a₂, l₂) (b l), có l₁ bước

Tổng cộng T(2) = l₁ + l₂ . (l₁ + 1)

Trường hợp n > 2: (b, l) (a₁, l₁) (a₂, l₂) … (a_n, l_n)

(a₁, l₁) (b, l) (a₂, l₂) … (a_n, l_n), vì b > a₁, có l₁ bước

(a₁, l₁) … (a_i-1, l_i-1) (b, l) (a_i, l_i) … (a_n, l_n), với 2 ≤ i ≤ n
- (a_i, 1) (a₁, l₁) … (a_i-1, l_i-1) (b, l) (a_i, l_i - 1) … (a_n, l_n), vì b > a_i, có 1 bước
- (a₁, l₁) … (a_i-1, l_i-1) (a_i, 1) (b, l) (a_i, l_i - 1) … (a_n, l_n)
  - xét mảng (a_i, 1) (a₁, l₁) … (a_i-1, l_i-1), lấy b = a_i, và n = i-1, được T(i-1) bước
- (a_i, 1) (a₁, l₁) … (a_i-1, l_i-1) (a_i, 1) (b, l) (a_i, l_i - 2) … (a_n, l_n), vì b > a_i, có 1 bước
- (a₁, l₁) … (a_i-1, l_i-1) (a_i, 2) (b, l) (a_i, l_i - 2) … (a_n, l_n), với b = a_i và n = i-1, được T(i-1) bước
- …
- (a_i, 1) (a₁, l₁) … (a_i-1, l_i-1) (a_i, l_i - 1) (b, l) … (a_n, l_n), có 1 bước
- (a₁, l₁) … (a_i-1, l_i-1) (a_i, l_i) (b, l) … (a_n, l_n), có T(i-1) bước
- tổng cộng = l_i . (T(i-1) + 1)

Tổng cộng
$T(n) = l_1 + \sum_{i=2}^{n}l_i(T(i-1)+1)$
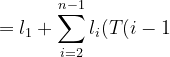$= l_1 + \sum_{i=2}^{n-1}l_i(T(i-1)+1) + l_n(T(n-1)+1) = T(n-1) + l_n(T(n-1)+1)$
$= (l_n+1)T(n-1) + l_n$

Từ hệ thức truy hồi T(n), chứng minh công thức tổng quát của T(n) bằng phương pháp quy nạp:
$T(n) = \prod_{i=1}^{n}\left( l_i+1 \right) - 1$

Bước cơ sở:
$T(1) = \prod_{i=1}^{1}(l_i+1)-1 = l_1$
$T(2) = \prod_{i=1}^{2}(l_i+1)-1 = (l_1+1)(l_2+1) - 1 = l_1 + l_2(l_1+1)$

Bước quy nạp (n ≥ 2):
$T(n+1) = (l_{n+1}+1)T(n) + l_{n+1}$
$= (l_{n+1}+1)\left[\prod_{i=1}^{n}(l_i+1) - 1\right ] + l_{n+1} = (l_{n+1}+1)\prod_{i=1}^{n}(l_i+1) - (l_{n+1}+1) + l_{n+1}$
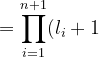$= \prod_{i=1}^{n+1}(l_i+1) - 1$

Xét một dạng mảng khác tổng quát hơn: (a₁, l₁) (a₂, l₂) … (a_k, l_k) (a_k+1, l_k+1) … (a_n, l_n) (b, l)

a₁ < a₂ < … < a_k < b < a_k+1 < … < a_n,
a_i, b, n là các số nguyên dương.

Sau khi sort, ta được mảng: (a₁, l₁) (a₂, l₂) … (a_k, l_k) (b, l) (a_k+1, l_k+1) … (a_n, l_n)

Gồm có 2 giai đoạn để sắp xếp mảng trên.
Giai đoạn 1: vì a_n > b nên (b, l) được chuyển đầu mảng, có l bước, thu được mảng

(b, l) (a₁, l₁) (a₂, l₂) … (a_k, l_k) (a_k+1, l_k+1)

Giai đoạn 2: chèn (b, l) vào giữa (a_k, l_k) và (a_k+1, l_k+1), số bước bằng T(k) (sắp xếp (b, l) vào mảng (a₁1, l₁) … (a_k, l_k)).

(a₁1, l₁) (a₂, l₂) … (a_k, l_k) (b, l) (a_k+1, l_k+1) … (a_n, l_n)

Tổng cộng: l + T(k)

Từ các tính toán trên, xây được giải thuật, trong đó inputs và arr là mảng các (a_i, l_i), inputs là mảng ban đầu, arr là mảng các phần tử đã được duyệt bởi vòng lặp for:

Nếu sử dụng giải thuật trên, for chạy trong O(n), lệnh gán count chạy trong O(n). Do đó, tổng cộng thời gian chạy là O(n²), không thoả mãn yêu cầu đề bài. Nên cần phải có cách để giảm lệnh cập nhật count từ O(n) xuống còn O(logn). Một cách giải quyết là sử dụng self-balancing tree.

Tree được xây dựng dựa trên ý tưởng của AVL Tree, nhưng thay vì các giá trị value được lưu trữ ở tất cả các node, thì tree có 2 loại node.

Leaf node: node lá lưu trữ giá trị chính, key là b và value là l+1. Nếu duyệt theo inorder traversing thì thứ tự các node lá in ra theo thứ tự tăng dần.
Node còn lại: node lưu trữ giá trị được tính từ các subtree (computed value), đại diện cho một tập các node lá.
- Giá trị [start, end] bao phủ tất cả giá trị key của các node lá, start cho giá trị key nhỏ nhất mà node bao phủ, end cho giá trị key lớn nhất mà node bao phủ.
- Giá trị value là tích các của các value của node lá.

Ví dụ:
BoiTree%20(1)

Node lá lần lượt lưu theo thứ tự từ trái sang phải: (0,3), (1,5), (2,4), (3,4), (5,3)
Node [0,1] bao phủ (0,3), (1,5), có value = 15 = 3.5
Node [0,2] bao phủ (0,3), (1,5), (2,4), có value = 60 = 15.4 = 3.5.4
Node [3,5] bao phủ (3,4), (5,3), có value = 12 = 4.3
Node [0,5] bao phủ (0,3), (1,5), (2,4), (3,4), (5,3), có value = 720 = 60.12 = (15.4) . (4.3) = 3.5.4.4.3

3 thao tác chính trên tree, mỗi thao tác đều là O(logn)

max: duyệt từ root sang nhánh phải liên tục đến khi gặp leaf node, trả về value của leaf node.
insert: cập nhật hoặc thêm node mới vào tree.
- nếu đã tồn tại key trong tree, cập nhật lại value của leaf node chứa key, cập nhật giá trị value của các node cha.
- nếu chưa tồn tại key, tạo node mới tạo vị trí leaf node có key gần bằng với key, cập nhật các node cha, tự động chỉnh tree cân bằng nếu tạo node làm mất cân bằng tree.
count: Trả về giá trị tích (l_i + 1)-1, có a_i nhỏ hơn key = b. Ví dụ count(4)
- count(4) = count([0,2]) * count[3,4]) - 1
- count([0,2]) = 60
- count([3,4]) = count((3,4)) = 4
- count(4) = 60 * 4 - 1 = 240 - 1 = 239