H mình mới hiểu 
Xét trong R^2 thôi.
Đầu tiên có phép nhân [1 0 | 0 1] X [2 | 5] = [2 | 5]. [1 0 | 0 1] gồm [1 | 0] và [0 | 1] quen thuộc.
[2 1 | 7 8] đại diện cho basis [2 | 7] và [1 | 8].
Vậy (2, 5) trong basis tạo bởi (2, 7) và (1, 8) là:
2*(2, 7) + 5*(1, 8)
= (2*2, 2*7) + (5*1, 5*8)
= (2*2 + 5*1, 2*7 + 5*8)
= (9, 54)
Nhưng nếu (2, 7) và (1, 8) này lại theo một cơ sở không chính tắc, vd như (1, 4) và (3, 2) thì ta phải viết nó theo cơ sở chính tắc, hay [1 3 | 4 2] * [2 1 | 7 8].
Vậy đặt A = [1 3 | 4 2] và B = [2 1 | 7 8] ta có tích (A*B)*v. Theo tc kết hợp còn có thể nhìn theo 1 cách khác là (v trong cơ sở bởi B) ở cơ sở bởi A. Nhưng nó lại cùng là một vector  khá khó hình dung.
khá khó hình dung.
Ma trận I[3*3] gồm 3 vector cột (1, 0, 0) (0, 1, 0) (0, 0, 1) hợp thành cơ sở chính tắc (hiểu là mặc định) cho R^3 (dễ thấy (a, b, c) = a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1))
Đó là với [NN] * [Nq]. Còn [a*b] * [b*c]?
[a*b] chính là b vector trong R^a. Mỗi vector cột của ma trận bên phải [b*c] chỉ ra một cách kết hợp (linear combination) những vector này thành một vector mới.
Nếu b < a thì ma trận bên trái biểu diễn 1 không gian con b chiều trong R^a. Có khái niệm span(v1, v2, …, vn) (vector nhé) chính là chỉ không gian đấy.
(mình thì mình ko hiểu cách ở #20 cho lắm)
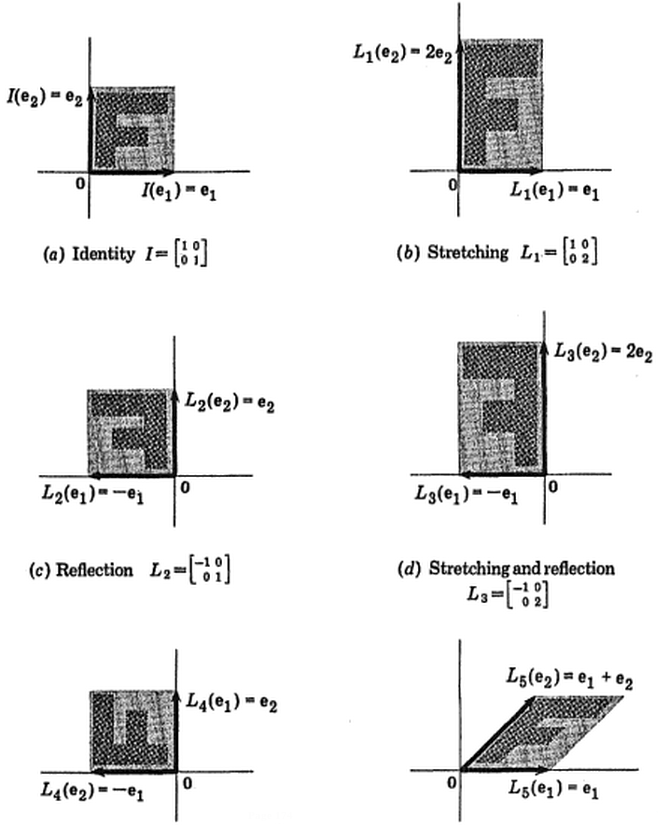


 khá khó hình dung.
khá khó hình dung. Em cũng có thắc mắc tương tự như bác, đọc cmt của mọi người và đã hiểu ý nghĩa của phép nhân ma trận
Em cũng có thắc mắc tương tự như bác, đọc cmt của mọi người và đã hiểu ý nghĩa của phép nhân ma trận 

 83% thành viên diễn đàn không hỏi bài tập, còn bạn thì sao?
83% thành viên diễn đàn không hỏi bài tập, còn bạn thì sao?